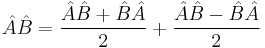Uncertainty principle derivations
There have been several mathematical improvements on the Heisenberg uncertainty principle. Since the time of the original formulation, the uncertainty relation has become increasingly nuanced; our understanding of it has undergone both a qualitative and a quantitative change. On the qualitative side, uncertainty is seen to have a broader scope than the limited version of Heisenberg's Gedankenexperiment; it is seen in terms of the multifaceted process of quantum measurement. On the quantitative side, Heisenberg's uncertainty principle has been translated into the more formal language of quantum mechanics and given various interpretations and reformulations.
The Heisenberg uncertainty relation and its more formal versions deal explicitly with the quantum operators for position, 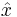 and for momentum,
and for momentum, 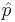 . Both the Robertson and Schrödinger uncertainty relations were derived for generalized quantum operators. Yet other formulations have moved beyond the framework which inspired these traditional uncertainty relations.
. Both the Robertson and Schrödinger uncertainty relations were derived for generalized quantum operators. Yet other formulations have moved beyond the framework which inspired these traditional uncertainty relations.
Contents |
The Heisenberg Uncertainty Relation
Heisenberg originally thought of uncertainty in an intuitive way. He pictured a microscope through which one could view very small objects. Heisenberg proposed a Gedankenexperiment in which one uses high-frequency photons to improve the resolution of what is being imaged. In his seminal paper on uncertainty[1][2] Heisenberg explains, "Let one illuminate the electron and observe it under a microscope. Then the highest attainable accuracy in the measurement of position is governed by the wavelength of the light. However, in principle one can build, say, a gamma-ray microscope and with it carry out the determination of position with as much accuracy as one wants." However, he notes, since gamma rays have high-frequency and energy, they will greatly disturb the electron being observed. The observed electron undergoes "a discontinuous change of momentum." Essentially, it is a Catch-22; the high-frequency gamma ray determines the position very accurately, yet it disturbs the electron so much that one loses track of the momentum. Likewise, if one uses lower frequency photons, such as microwaves, the momentum will be much more certain, but the position will become fuzzy. All of this is encapsulated in his uncertainty principle
where 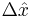 is the uncertainty of knowledge about the position of the particle,
is the uncertainty of knowledge about the position of the particle, 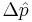 is the uncertainty associated with the momentum of the particle, and
is the uncertainty associated with the momentum of the particle, and  is the Planck constant. Max Planck had introduced
is the Planck constant. Max Planck had introduced  to describe the smallest possible amount of "action" (energy multiplied by time) involved in quantum processes[3] and Heisenberg used this as his lower bound.
to describe the smallest possible amount of "action" (energy multiplied by time) involved in quantum processes[3] and Heisenberg used this as his lower bound.
After Heisenberg formulated his equation, Kennard[4] and later Weyl derived [5] the more formal relation
where 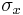 and
and 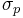 are standard deviations of the two operators
are standard deviations of the two operators 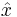 and
and 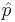 defined for an arbitrary Hermitian operator
defined for an arbitrary Hermitian operator 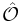 as
as
-
-
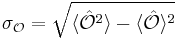 .
.
-
The Robertson and Schrödinger Uncertainty Relations
The Robertson Uncertainty Relation
Going even further, Robertson[6] generalized Weyl's equation for arbitrary Hermitian operators 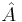 and
and 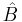
where 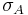 and
and 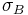 are the standard deviations and where
are the standard deviations and where ![[\hat{A},\hat{B}]](/2012-wikipedia_en_all_nopic_01_2012/I/c081d8bf21108f8283f018b863a75393.png) represents the commutator
represents the commutator ![[\hat{A},\hat{B}]\equiv \hat{A}\hat{B}-\hat{B}\hat{A}](/2012-wikipedia_en_all_nopic_01_2012/I/dd1ee0e2ae3e8813042ecdae64ed02e9.png) or the incompatibility of the two operators
or the incompatibility of the two operators 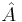 and
and 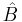 . The majority of quantum textbooks rederive the Robertson uncertainty relation when presenting a generalized derivation of the uncertainty principle (see, for example,[7][8][9]).
. The majority of quantum textbooks rederive the Robertson uncertainty relation when presenting a generalized derivation of the uncertainty principle (see, for example,[7][8][9]).
| Derivation of the Robertson uncertainty relation | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
The derivation shown here follows the derivation in Griffiths.[10] For any Hermitian operator  (dropping the operator hat (dropping the operator hat 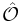 notation), based upon the standard deviation definition, we have notation), based upon the standard deviation definition, we have
we let Similarly, for any other Hermitian operator for The product of the two deviations can thus be expressed as
In order to relate the two vectors
and thus Eq. (1) can be written as
Since
we let
The inner product and using the fact that Similarly it can be shown that We now substitute the above equation above back into Eq. (4) and get Substituting the above into Eq. (2) we get the Robertson uncertainty relation |
The Schrödinger Uncertainty Relation
Though Heisenberg's uncertainty principle and Robertson's version of the uncertainty relation are part of the foundation of quantum mechanics, other versions of the uncertainty relation-including the Schrödinger uncertainty relation-have received comparatively little attention in the physics literature. The Schrödinger uncertainty relation was initially published in an inconspicuous German journal[12] that periodically reported on the activity of the Prussian Academy.[13] This may have led to the cursory coverage the Schrödinger uncertainty relation receives in the literature.
Schrödinger derived the following uncertainty relation
The difference between Schrödinger's and Robertson's version is the first squared term under the square root, known in a classical statistics sense as the covariance, consisting of the anti-commutator 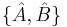 , defined as
, defined as 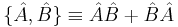 , and the product of two expectation values
, and the product of two expectation values 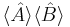 . As pointed out originally by Schrödinger,[14] the Schrödinger uncertainty relation often has the effect of raising the lower bound on uncertainty. Because the added terms are squared, the Schrödinger additions are either positive or zero. This will obviously either increase the uncertainty by some amount, or make no difference.
. As pointed out originally by Schrödinger,[14] the Schrödinger uncertainty relation often has the effect of raising the lower bound on uncertainty. Because the added terms are squared, the Schrödinger additions are either positive or zero. This will obviously either increase the uncertainty by some amount, or make no difference.
| Derivation of the Schrödinger uncertainty relation | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
The derivation shown here incorporates and builds off of those done in Robertson,[15] Schrödinger[16] and Griffiths.[17] For any Hermitian operator  (dropping the operator hat (dropping the operator hat 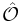 notation), based upon the standard deviation definition, we have notation), based upon the standard deviation definition, we have
we let Similarly, for any other Hermitian operator for The product of the two deviations can thus be expressed as
In order to relate the two vectors
and thus Eq. (1) can be written as
Since
we let
The inner product and using the fact that Similarly it can be shown that and We now substitute the above two equations above back into Eq. (4) and get Substituting the above into Eq. (2) we get the Schrödinger uncertainty relation |
It can also be shown[19] that the Schrödinger uncertainty relation for mixed states is given by
Discussion of the Schrödinger Uncertainty Relation
An analysis of the derivations of uncertainty reveals that uncertainty first comes into play with the Schwarz inequality and the related inequality for mixed states. In the context of the uncertainty principle, the Schwarz inequality was used first by Weyl[20] in his 1928 derivation of 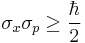 in which he sought (at the suggestion of Wolfgang Pauli) to relate the two standard deviations
in which he sought (at the suggestion of Wolfgang Pauli) to relate the two standard deviations 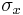 and
and 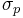 . The Schwarz inequality was also used by Robertson in his 1929 derivation and Schrödinger in his 1930 derivation, who both cite Weyl.
. The Schwarz inequality was also used by Robertson in his 1929 derivation and Schrödinger in his 1930 derivation, who both cite Weyl.
Schrödinger's method of derivation differed from that of Robertson. The critical step that differentiates the two is Schrödinger's use of the fact that the product of two Hermitian operators is not in general Hermitian, but can be split into a "symmetric product and half its commutator"[21]:
Schrödinger then comments that this splitting corresponds to a splitting of a complex number into real and imaginary parts, and thus an expectation value can also be split into real and imaginary parts. This corresponds directly to Eq. (3) from the boxed derivations above. If one takes only the imaginary part, one recovers the Robertson relation; if one takes both the real and imaginary parts, the Schrödinger relation results.
See also
References
- ^ Heisenberg, W. (1927). "Uber die Grundprinzipien der Quantenmechanik". Forsch. Fortschr. 3: 83.
- ^ Wheeler, J.A. (1983). Quantum Theory and Measurement. Princeton, NJ: Princeton UP. pp. 64.
- ^ Planck, M. (1901). "Ueber das Gesetz der Energieverteilung im Normalspectrum". Ann. Phys. 309: 553–563.
- ^ Kennard, E. H. (1927), "Zur Quantenmechanik einfacher Bewegungstypen", Zeitschrift für Physik 44 (4–5): 326, Bibcode 1927ZPhy...44..326K, doi:10.1007/BF01391200.
- ^ Weyl, H. (1928). Gruppentheorie Und Quantenmechanik. Leipzig: Hirzel.
- ^ Robertson, H. P. (1929). "The Uncertainty Principle". Phys. Rev. 43: 163–64.
- ^ Griffiths, David (2005). Quantum Mechanics. New Jersey: Pearson.
- ^ Townsend, J.S. (2000). A Modern Approach to Quantum Mechanics. University Science Books.
- ^ Liboff, R.L. (2002). Introductory Quantum Mechanics. Addison Wesley.
- ^ Griffiths, David (2005). Quantum Mechanics. New Jersey: Pearson.
- ^ Riley, K. F.; M. P. Hobson and S. J. Bence (2006). Mathematical Methods for Physics and Engineering. Cambridge. pp. 246.
- ^ Schrödinger, E. (1930). "Zum Heisenbergschen Unschärfeprinzip". Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse 14: 296–303.
- ^ Angelow, A. (2007). "Evolution of Schrödinger Uncertainty Relation in Quantum Mechanics". arXiv:0710.0670.
- ^ Schrödinger, E. (1930). "Zum Heisenbergschen Unschärfeprinzip". Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse 14: 296–303.
- ^ Robertson, H. P. (1929). "The Uncertainty Principle". Phys. Rev. 43: 163–64.
- ^ Schrödinger, E. (1930). "Zum Heisenbergschen Unschärfeprinzip". Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse 14: 296–303.
- ^ Griffiths, David (2005). Quantum Mechanics. New Jersey: Pearson.
- ^ Riley, K. F.; M. P. Hobson and S. J. Bence (2006). Mathematical Methods for Physics and Engineering. Cambridge. pp. 246.
- ^ Steiger, Nathan. "Quantum Uncertainty and Conservation Law Restrictions on Gate Fidelity". Brigham Young University. http://www.physics.byu.edu/Thesis/view.aspx?id=270. Retrieved 19 June 2011.
- ^ Weyl, H. (1928). Gruppentheorie Und Quantenmechanik. Leipzig: Hirzel.
- ^ Angelow, A.; M. Batoni (1999). "Translation with Annotation of the Original Paper of Erwin Schrodinger (1930) in English". Bulg. J. Phys. 26: 193–203.
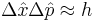
![\sigma_{A}\sigma_{B} \geq\frac{1}{2i}\langle[\hat{A},\hat{B}]\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/8d3fd1291b19e4cb295cd3f731caa96d.png)
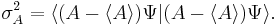
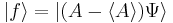 and thus
and thus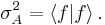
 in the same state
in the same state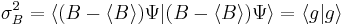
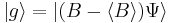 .
.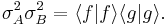
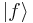 and
and 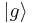 , we use the Schwarz inequality
, we use the Schwarz inequality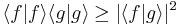 ,
,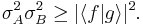
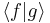 is in general a complex number, we use the fact that the modulus squared of any complex number
is in general a complex number, we use the fact that the modulus squared of any complex number  is defined as
is defined as 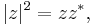 where
where 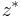 is the complex conjugate of
is the complex conjugate of 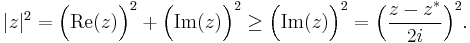
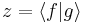 and
and 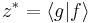 and substitute these into the equation above to get
and substitute these into the equation above to get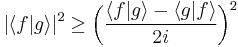
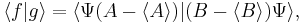
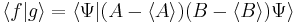
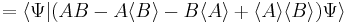
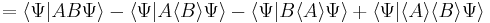
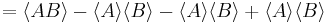
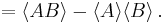
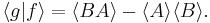 Thus we have
Thus we have![\langle f|g\rangle-\langle g|f\rangle = \langle AB\rangle-\langle A\rangle\langle B\rangle-\langle BA\rangle%2B\langle A\rangle\langle B\rangle = \langle [A,B]\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/93f65f5658b57bdddd436ddb36604b5a.png)
![|\langle f|g\rangle|^{2}\geq\Big(\frac{1}{2i}\langle[A,B]\rangle\Big)^{2} .](/2012-wikipedia_en_all_nopic_01_2012/I/28f5218fd91a3510698aab3b169c1d65.png)
![\sigma_{A}\sigma_{B} \geq \frac{1}{2i}\langle[A,B]\rangle .](/2012-wikipedia_en_all_nopic_01_2012/I/8ed192d73defc056808f8e325c7d2d87.png)
![\sigma_{A}\sigma_{B} \geq \sqrt{\Big(\frac{1}{2}\langle\{\hat{A},\hat{B}\}\rangle - \langle \hat{A} \rangle\langle \hat{B}\rangle\Big)^{2}%2B \Big(\frac{1}{2i}\langle[\hat{A},\hat{B}]\rangle\Big)^{2}}.](/2012-wikipedia_en_all_nopic_01_2012/I/1fbade92cbb358a627fe8884b89255f2.png)
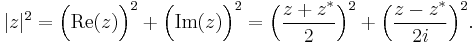
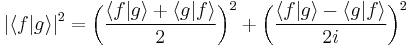
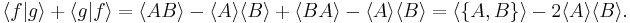
![|\langle f|g\rangle|^{2}=\Big(\frac{1}{2}\langle\{A,B\}\rangle - \langle A \rangle\langle B\rangle\Big)^{2}%2B \Big(\frac{1}{2i}\langle[A,B]\rangle\Big)^{2}\, .](/2012-wikipedia_en_all_nopic_01_2012/I/633fd9da73bd2e02368c9f7665b37efb.png)
![\sigma_{A}\sigma_{B} \geq \sqrt{\Big(\frac{1}{2}\langle\{A,B\}\rangle - \langle A \rangle\langle B\rangle\Big)^{2}%2B \Big(\frac{1}{2i}\langle[A,B]\rangle\Big)^{2}}\, .](/2012-wikipedia_en_all_nopic_01_2012/I/00735bcda8289f2f0e202b105a308fa5.png)
![\sigma_{A}^{2}\sigma_{B}^{2}\geq \bigg(\frac{1}{2}Tr(\rho\{A,B\})-Tr(\rho A)Tr(\rho B)\bigg)^{2}%2B\bigg(\frac{1}{2i}Tr(\rho[A,B])\bigg)^{2}](/2012-wikipedia_en_all_nopic_01_2012/I/5d4b7932c249111702f013fb1165575b.png)